2. Chyby a nestabilita#

Naimportujeme si knihovny potřebné pro následující příklady:

import numpy as np
import matplotlib.pyplot as plt

2.1. Chyby - nepřesnosti při řešení numerických úloh#

Zdroje chyb:

  1. Chyby vstupních dat (např. chyby měření, chyby modelu reality)

  2. Zaokrouhlovací chyby (roundoff errors) - v důsledku zaokrouhlování při výpočtech s čísly o konečné délce

  3. Chyby metody (truncation errors) - v důsledku převedení matematické úlohy na numerickou

2.1.1. Relativní a absolutní chyba#

  • absolutní chyba \(= \|\)přesná hodnota - přibližná hodnota\(\|\)

  • \(A(x) = \| x -\tilde{x}\|\)

  • relativní chyba \(=\) absolutní chyba / \(\|\)přesná hodnota\(\|\)

  • \(R(x) = \dfrac{A(x)}{\| x\|}\)

2.1.2. Zaokrouhlovací chyby#

2.1.2.1. Reprezentace reálných čísel v počítači#

  • floating point (pohyblivá desetinná čárka): \(\pm 1.23456789\times10^{\pm21}\) (znaménko \(\pm\); mantisa 1.23456789; exponent \(\pm21\))

  • délka exponentu určuje rozsah

  • délka manitsy určuje přesnost

  • v počítači je mezi 1 a 2 je konečný počet čísel 1, 1+\(\epsilon\), 1+\(2\epsilon\),…,2-\(\epsilon\)

  • čím menší \(\epsilon\), tím menší jsou chyby v zaokrouhlování

  • chyby při arimetických výpočtech v počítačích mohou mít své důsledky [1, 2]

Cvičení 02.01: Odhadněte $\epsilon$ a odhad porovnejte se skutečnou hodnotou.

Budeme postupovat tak, že počáteční odhad (libovolně vysoký) budeme postupně dělit dvěma tak dlouho, dokud po přičtení k jedničce dostaneme číslo větší než jedna.

# kod
cislo = 1.0           # Absolutni hodnota epsilon je ruzna pro ruzna cisla
eps   = 0.1 * cislo # Pocatecni odhad epsilon
# Zmensujeme eps, dokud po jeho pricteni ke vstupnimu cislu dostavame vetsi cislo
# Odhad bude presny v ramci jednoho radu (ve dvojkove soustave, tj. muze se 2x lisit)
while ( cislo+eps > cislo ):
    eps = eps / 2  # Pro nasledujici iteraci vyzkousime polovicni eps

#Posledni iterace jiz hodnotu nezmenila, potrebujeme hodnotu z predposledni
# iterace - ta je rovna dvojnasobku aktualni hodnoty eps.
eps = 2 * eps

print('Odhad strojoveho epsilon je: ',eps)

#  Knihovna nupmy ma definovane skutecne hodnoty strojoveho epsilon.
print('Skutecna hodnota epsilon je: ',np.finfo(float).eps)

Odhad strojoveho epsilon je:  1.7763568394002506e-16
Skutecna hodnota epsilon je:  2.220446049250313e-16

2.1.2.2. Šíření chyb ve výpočtech#

Motivace pro numerické postupy: vyhnout se odečítání dvou přibližně stejně velkých čísel:

# kod
a = 4.9
b = 4.845
c = a - b
print(c)

0.055000000000000604

  • V počítači nemusí platit \((a + 1) - 1 = a\)

Cvičení 02.02: Vypočítejte 1 + 1/3 - 1/3. Ověřte výsledek i pro případ, že byste přičtení i odečtení provedli 100x.
# kod
def pricist_a_odecist(n):
    vysledek = 1.0
    
    for i in range(n):
        vysledek += 1/3

    for i in range(n):
        vysledek -= 1/3
        
    return vysledek

#1x
print(1+1/3-1/3)
# 100x
pricist_a_odecist(100)

1.0

1.0000000000000002

  • V počítači nemusí platit asociativnost sčítání \((a+b)+c = a+(b+c)\).

Cvičení 02.03: Mějme řadu definovanou jako $x_{n} = \exp(-n\ln(1,1))$. Sečtěte prvních 30 členů v jednom směru a v druhém směru.
# kod
# Vrati i-ty prvek rady
def rada(i):
    return np.exp(-i*np.log(1.1))

# Secte radu vzestupne od 0 do n
def soucet_vzestupne(n):
    soucet = 0   # Nezapominejte na inicializaci hodnoty promenne
    for i in range(n+1):
        soucet = soucet + rada(i)
    return soucet


# Secte radu sestupne od n do 0
def soucet_sestupne(n):
    soucet = 0
    for i in reversed(range(n+1)): #range(n,-1,-1):
        soucet = soucet + rada(i)
    return soucet

n = 30
print(soucet_vzestupne(n))
print(soucet_sestupne(n))

10.426914466988315
10.426914466988313

2.1.3. Chyba metody#

  • Při výpočtech nahrazujeme nekonečně krátký krok \(dx\) krokem \(h\), který má konečnou délku.

2.1.3.1. Taylorův rozvoj#

  • \(f(x+h)=\sum_{n}\dfrac{h^{n}f^{(n)}(x)}{n!}\)

  • Řád metody \(\alpha\): chyba veličiny úměrná \(h^{\alpha}\)

2.1.3.1.1. Metoda prvního řádu (dopředná diference)#

  • \(f(x+h)=f(x)+hf'(x) + \mathcal{O}(h^{2})\rightarrow f'(x)=\dfrac{f(x+h)-f(x)}{h} + \dfrac{\mathcal{O}(h^{2})}{h}\rightarrow f'(x)=\dfrac{f(x+h)-f(x)}{h} +\mathcal{O}(h)\)

  • získám aproximaci derivace \(f'(x)\approx\dfrac{f(x+h)-f(x)}{h}\), přičemž zanedbám \(\mathcal{O}(h)\)

2.1.3.1.2. Metoda druhého řádu (centrální diference)#

  • \(f(x+h)=f(x)+hf'(x) + \dfrac{h^{2}}{2}f''(x)+\mathcal{O}(h^{3})\)

  • \(f(x-h)=f(x)-hf'(x) + \dfrac{h^{2}}{2}f''(x)+\mathcal{O}(h^{3})\)

  • odečtením těchto dvou rovnic získám aproximaci derivace \(f'(x)\approx\dfrac{f(x+h)-f(x-h)}{2h}\), přičemž zanedbám \(\mathcal{O}(h^{2})\)

Cvičení 02.04: Spočtěte numericky derivaci funkce $\sin(x)$ v bodě $x=\pi/6$ pomocí dopředné a centrální diference pro velikost kroku $h\in(\epsilon,\pi/6\rangle $. Zobrazte výsledek a velikost relativní chyby v závislosti na $h$.

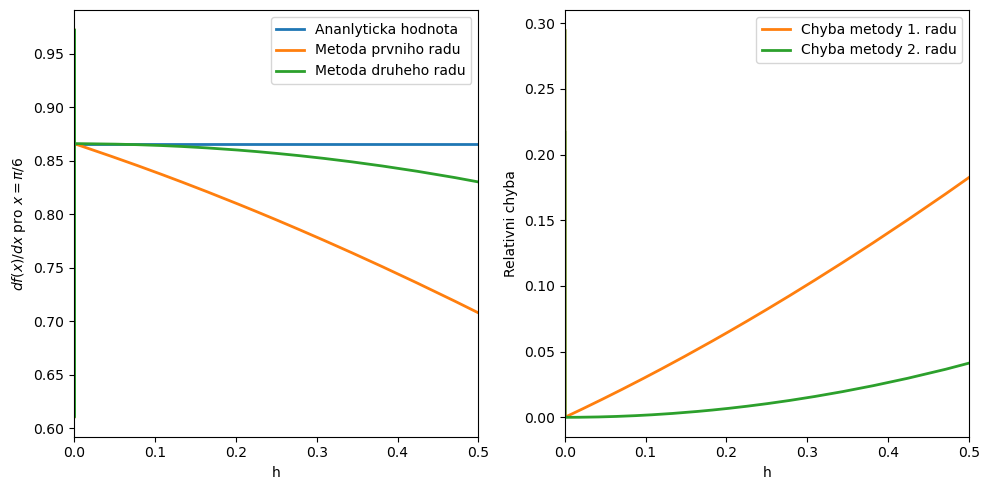
Měli bychom dojít k výsledku \(\sqrt{3}/2\approx 0.866\), což mohu ověřit zadáním derivative of sin(x) at x=pi/6 do WolframAlpha.

# kod

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return np.sin(x)

def df(x):
    return np.cos(x)

def num1_df(x, h):
    return (f(x+h) - f(x))/h

def num2_df(x, h):
    return (f(x+h) - f(x-h))/(2*h)

x = np.pi/6
h = x  # Pocatecni hodnota h

der_a = df(x) # Hodnota derivace analyticky
der_1 = num1_df(x,h) # Derivace metodou prvniho radu
der_2 = num2_df(x,h) # Derivace metodou druheho radu
krok  = h # Seznam pouzitych velikosti kroku

# Hledame hodnoty derivace v bode x v zavislosti na kroku h
while h > np.finfo(float).eps:
    der_a = np.append(der_a, df(x))
    der_1 = np.append(der_1, num1_df(x,h))
    der_2 = np.append(der_2 ,num2_df(x,h))
    krok  = np.append(krok, h)
    h = 0.9 * h

fig, ax = plt.subplots(1,2,figsize=(10,5))
ax[0].plot(krok,der_a,linewidth=2,label='Ananlyticka hodnota')
ax[0].plot(krok,der_1,linewidth=2,label='Metoda prvniho radu')
ax[0].plot(krok,der_2,linewidth=2,label='Metoda druheho radu')
ax[0].set_xlabel('h')
ax[0].set_ylabel(r'$df(x)/dx$ pro $x=\pi/6$')
ax[0].set_xlim((0,0.5))
#ax[0].set_xscale('log')
ax[0].legend()

ax[1].plot(krok, np.abs((der_1-der_a)/der_a),c='C1',linewidth=2,label='Chyba metody 1. radu')
ax[1].plot(krok, np.abs((der_2-der_a)/der_a),color='C2',linewidth=2,label='Chyba metody 2. radu')
ax[1].set_xlabel('h')
ax[1].set_ylabel('Relativni chyba')
ax[1].set_xlim((0,0.5))
ax[1].legend()

fig.tight_layout()
_images/Cviceni02vyplnene_24_0.png

2.2. Numerická stabilita#

Cvičení 02.05: Pomocí a) Eulerovy a b) dvoukrokové metody vypočítejte časový vývoj rychlosti meteoritu, který je v atmosféře exponenciálně brzděn, přičemž $v(0)=1$.

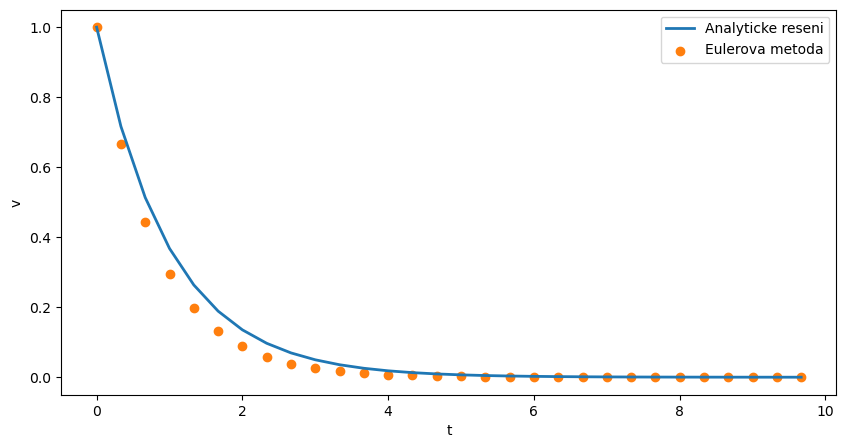
Rychlost meteoritu lze popsat diferenciální rovnicí \(\dfrac{dv}{dt}=-v(t)\). Jejím řešením je \(v(t)=K\exp(-t)\). Konstatu \(K\) najdeme pomocí počáteční podmínky \(v(0)=1\), a tedy \(K=1\).

  • a) Eulerova metoda (dopředná diference)

  • derivaci nahradíme konečnou diferencí: \(\dfrac{v(t+dt)-v(t)}{dt}=-v(t)\)

  • odtud získám rychlost \(v\) v čase \(t+dt\): \(v(t+dt)=-v(t)dt+v(t)\)

T = 10
N = 30
dt = T/N

t = np.empty(N)
v = np.empty(N)
v_exact = np.empty(N)

# pocatecni podminky
t[0] = 0
v[0] = 1

# presne reseni
v_exact[0] = np.exp(-t[0])

# diferencni schema v(t+dt)-v(t)/dt = -v(t)
for i in range (1,N):
    t[i] = t[i-1] + dt
    v[i] = -v[i-1]*dt + v[i-1]
    v_exact[i] = np.exp(-t[i])

fig, ax = plt.subplots(figsize=(10,5))    
ax.plot(t,v_exact,label='Analyticke reseni',linewidth=2)
ax.scatter(t,v,label='Eulerova metoda',color='C1')
ax.set_xlabel('t')
ax.set_ylabel('v')
ax.legend()

<matplotlib.legend.Legend at 0x71c82029ee80>
_images/Cviceni02vyplnene_29_1.png

  • b) Dvoukroková metoda (centrální diference)

  • derivaci nahradíme centrální diferencí s dvojnásobným krokem: \(\dfrac{v(t+dt)-v(t-dt)}{2dt}=-v(t)\)

  • odtud získám rychlost \(v\) v čase \(t+dt\): \(v(t+dt)=-2v(t)dt+v(t-dt)\)

T = 10
N = 30
dt = T/N

t = np.empty(N)
v = np.empty(N)
v_exact = np.empty(N)

# pocatecni podminky
t[0] = 0
v[0] = 1

# druhy casovy krok
t[1] =t[0] + dt

# presne reseni v prvnich dvou bodech
v_exact[0] = np.exp(-t[0])
v_exact[1] = np.exp(-t[1])

# schema je tribodove, takze poterbujeme jeste jednu hodnotu v(2)
v[1] = v_exact[1]

# diferencni schema v(t+dt)-v(t-dt)/2dt = -v(t)
for i in range (2,N):
    t[i] = t[i-1] + dt
    v[i] = -2*v[i-1]*dt + v[i-2] 
    v_exact[i] = np.exp(-t[i])

    
fig, ax = plt.subplots(figsize=(10,5))    
ax.plot(t,v_exact,label='Analyticke reseni',linewidth=2)
ax.scatter(t,v,label='Dvoukrokova metoda',color='C1')
ax.set_xlabel('t')
ax.legend()

<matplotlib.legend.Legend at 0x71c820262910>
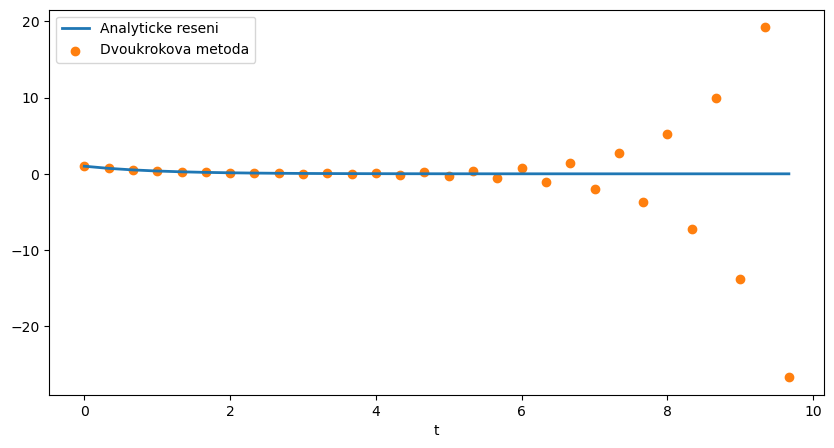
_images/Cviceni02vyplnene_31_1.png

Velikost chyby se postupně zvyšuje, jedná se tedy o nestabilní metodu, viz vysvětlení.