Řešení nelineárních rovnic
Contents
7. Řešení nelineárních rovnic#
Naimportujeme si knihovny potřebné pro následující příklady:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
numerické řešení nelineární rovnice je vždy iterační
řešení nejdříve odhadneme, pak ho postupně zpřesňujeme
7.1. Řešení jedné nelineární rovnice#
řešíme \(f(x)=0\) (řešení se často nazývá kořen)
postup:
ohraničení kořenů - určení intervalů, které obsahují jeden kořen
pokud pro \(x_{1}<x_{2}\) platí, že \(f(x_{1})f(x_{2})<0\), pak je v intervalu \((x_{1},x_{2})\) alespoň jeden kořen
zpřesňování hodnoty kořene
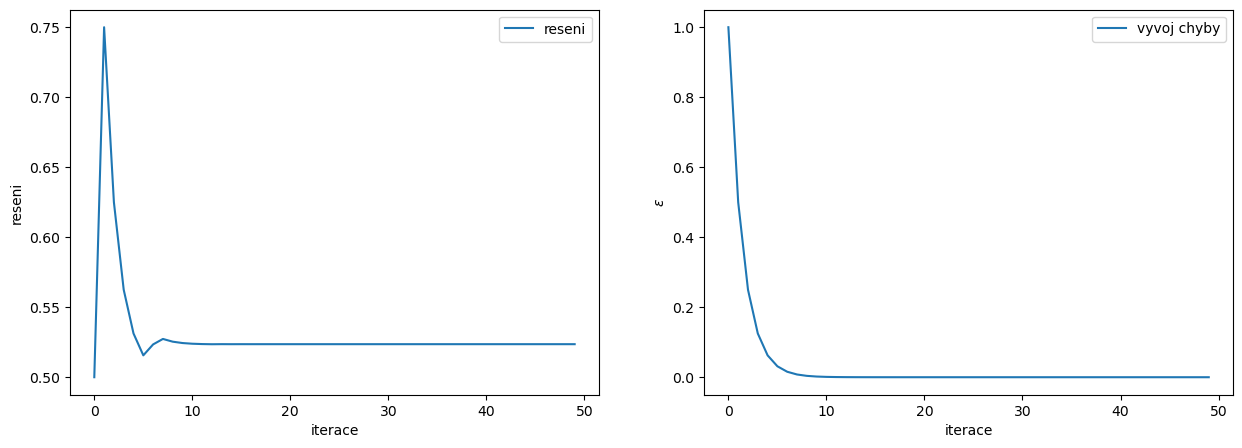
7.1.1. Metoda půlení intervalu#
postup
nechť je kořen ohraničen \(\langle a_{0},b_{0}\rangle\) tak, že platí \(f(a_{0})f(b_{0})<0\)
vypočítáme \(x_{1}=(a_{0}+b_{0})/2\)
jeden krajní bod ponecháme, druhý posuneme do \(x_{1}\), aby opět platilo \(f(a_{1})f(b_{1})<0\)
po \(n\)-tém kroku je kořen omezený body \(a_{n}\) a \(b_{n}\)
nepřesnost určení kořene: \(\epsilon = \lvert b_{n}-a_{n}\rvert\), přičemž \(\epsilon_{n+1}=\epsilon_{n}/2\)
spolehlivá metoda
v blízkosti kořene pomalá
#
# metoda puleni intervalu
# demonstrace metody puleni intervalu pro nelinearni rovnice
# nadefinujeme f(x) a budeme hledat reseni f(x)=0
def f(x):
return np.sin(x)-0.5
iteraci = 50 # celkovy pocet iteraci
# pocatecni body omezujici reseni
a = 0
b = 1
# budeme si prubezne ukladat odhad reseni a chybu odhadu
epsilon = np.zeros((iteraci)) # odhad chyby, tedy delku intervalu <a,b> v jednotlivych krocich
reseni = np.zeros((iteraci)) # aktualni odhad reseni
for i in range(iteraci):
c = (a+b)/2
epsilon[i] = b-a
reseni[i] = (a+b)/2
if f(a)*f(c)<0:
b = c
else:
a = c
koren = reseni[-1] # odhad konecneho reseni
chyba = epsilon[-1] # odhad konecne chyby
fig, ax = plt.subplots(1,2,figsize=(15,5))
# zobrazime vyvoj reseni v zavislosti na iteracich
ax[0].plot(range(iteraci),reseni,label='reseni')
ax[0].set_ylabel('reseni')
ax[0].set_xlabel('iterace')
ax[0].legend()
# zobrazime vyvoj chyby v zavislosti na iteracich
ax[1].plot(range(iteraci),epsilon,label='vyvoj chyby')
ax[1].set_ylabel(r'$\epsilon$')
ax[1].set_xlabel('iterace')
ax[1].legend()
# overeni reseni
spravne_reseni = fsolve(f, a)
print('f(x)=0 pro x= ',spravne_reseni)
f(x)=0 pro x= [0.52359878]
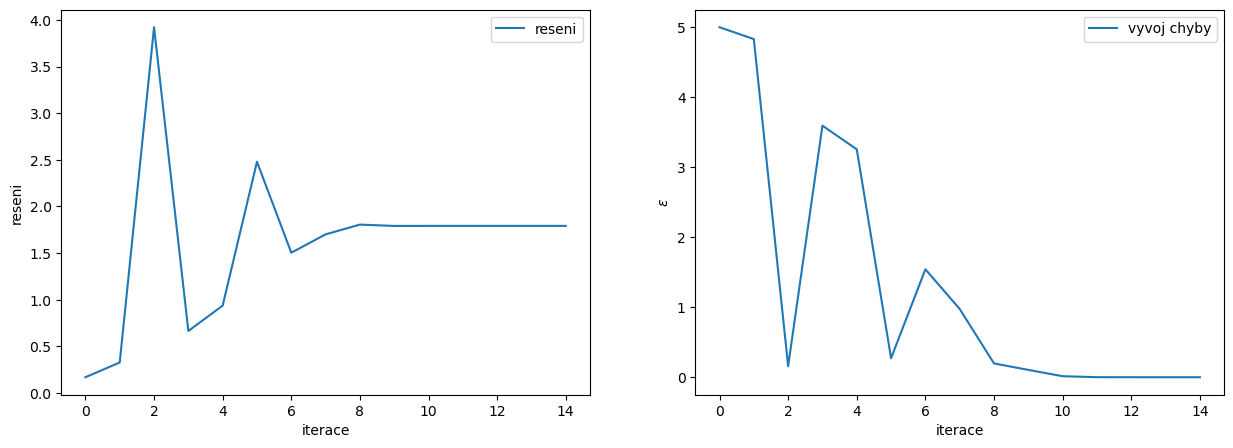
7.1.2. Metoda sečny#
postup
mějme body \(a_{n-1}\) a \(a_{n}\)
zvolíme \(a_{n+1}\) v průsečíku spojnice bodů \(\left(a_{n-1},y(a_{n-1})\right)\) a \(\left(a_{n},y(a_{n})\right)\) s osou \(x\)
konvergence není zaručena
#
# metoda secen
#demonstrace metody secen pro nelinearni rovnice
#spolu s odhadem radu metody
#nadefinujeme f(x) a budeme hledat reseni f(x)=0
def f(x):
return np.exp(x) - 6
iteraci = 15 # celkovy pocet iteraci
xi = 0 # pocatecni body omezujici reseni x(i)
xi_p1 = 5 # a x(i+1)
# budeme si prubezne ukladat odhad reseni a chybu odhadu
epsilon = np.zeros((iteraci)) # odhad chyby, tedy rozdil poslednich dvou odhadu korene
reseni = np.zeros((iteraci)) # aktualni odhad reseni
a = xi_p1
for i in range(iteraci):
c = (xi*f(xi_p1)-f(xi)*xi_p1)/(f(xi_p1)-f(xi))
epsilon[i] = np.abs(xi-xi_p1)
xi = xi_p1
xi_p1 = c
reseni[i] = c
koren = reseni[-1] # odhad konecneho reseni
chyba = epsilon[-1] # odhad konecne chyby
fig, ax = plt.subplots(1,2,figsize=(15,5))
# zobrazime vyvoj reseni v zavislosti na iteracich
ax[0].plot(range(iteraci),reseni,label='reseni')
ax[0].set_ylabel('reseni')
ax[0].set_xlabel('iterace')
ax[0].legend()
# zobrazime vyvoj chyby v zavislosti na iteracich
ax[1].plot(range(iteraci),epsilon,label='vyvoj chyby')
ax[1].set_ylabel(r'$\epsilon$')
ax[1].set_xlabel('iterace')
ax[1].legend()
# overeni reseni
spravne_reseni = fsolve(f, a)
print('f(x)=0 pro x= ',spravne_reseni)
f(x)=0 pro x= [1.79175947]
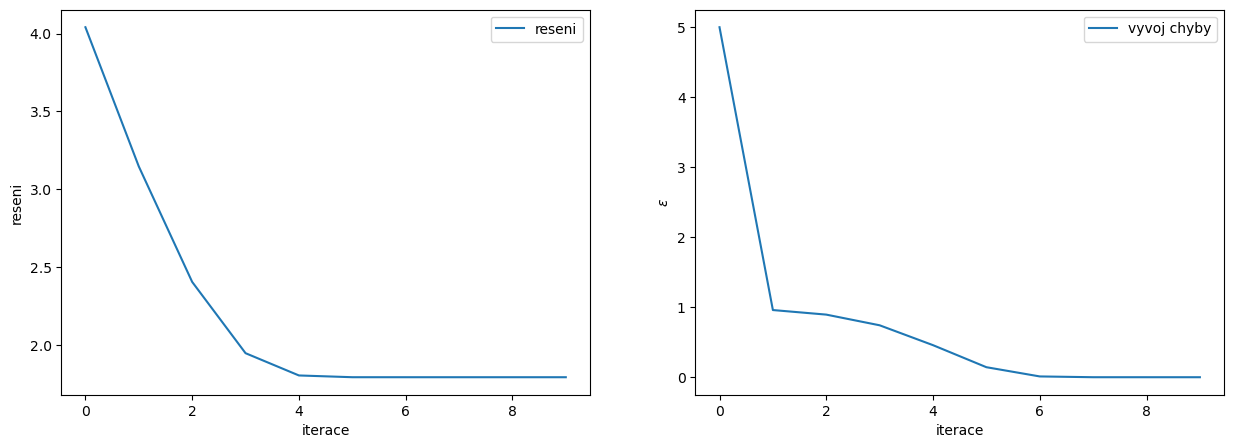
7.1.3. Metoda regula falsi#
modifikace metody sečen
po určení \(a_{n+1}\) si k němu vyberu z \(a_{n-1}\) a \(a_{n}\) takový bod \(\tilde{a}_{n}\), aby kořen zůstal ohraničený, tj. \(f(\tilde{a}_{n})f(a_{n+1})<0\)
konvergence je zaručena
7.1.4. Newton–Raphsonova (tečnová) metoda#
využívá první derivaci zadané funkce (je vhodná, pokud umíme hodnoty derivací rychle počítat)
Taylorův rozvoj zadané funkce v okolí bodu \(x_{i}\): $\( f(x_{i}+\delta)=f(x_{i})+\delta f'(x_{i})+\dfrac{\delta^{2}}{2}f''(x_{i})+\dots \)$
vypočítáme \(\delta\) z podmínky \(f(x)=0\)
iterační vzorec: \(x_{i+1}=x_{i}-\dfrac{f(x_{i})}{f'(x_{i})}\)
konvergence není zaručena
# metoda tecny
#demonstrace metody tecen pro nelinearni rovnice
#spolu s odhadem radu metody
# nadefinujeme f(x) a budeme hledat reseni f(x)=0
def f(x):
return np.exp(x) - 6
# derivace
def df(x):
return np.exp(x)
iteraci=10 # celkovy pocet iteraci
xi = 0 # pocatecni body omezujici reseni x(i)
xi_p1 = 5 # a x(i+1)
# budeme si prubezne ukladat odhad reseni a chybu odhadu
epsilon = np.zeros((iteraci)) # odhad chyby, tedy rozdil poslednich dvou odhadu korene
reseni = np.zeros((iteraci)) # aktualni odhad reseni
for i in range(iteraci):
c = xi_p1-f(xi_p1)/df(xi_p1)
epsilon[i] = np.abs(xi-xi_p1)
xi = xi_p1
xi_p1 = c
reseni[i] = c
koren = reseni[-1] # odhad konecneho reseni
chyba = epsilon[-1] # odhad konecne chyby
fig, ax = plt.subplots(1,2,figsize=(15,5))
# zobrazime vyvoj reseni v zavislosti na iteracich
ax[0].plot(range(iteraci),reseni,label='reseni')
ax[0].set_ylabel('reseni')
ax[0].set_xlabel('iterace')
ax[0].legend()
# zobrazime vyvoj chyby v zavislosti na iteracich
ax[1].plot(range(iteraci),epsilon,label='vyvoj chyby')
ax[1].set_ylabel(r'$\epsilon$')
ax[1].set_xlabel('iterace')
ax[1].legend()
# overeni reseni
spravne_reseni = fsolve(f, a)
print('f(x)=0 pro x= ',spravne_reseni)
f(x)=0 pro x= [1.79175947]
7.1.5. Mullerova metoda#
# Mullerova metoda
def f(x):
return 4*x**3 - 2*x**2 - 4*x - 3
# pozadovana presnost
presnost = 1.0e-6
n = 1
# známe 3 body a odpovídající 3 funkční hodnoty
x1 = 1
x2 = 2
x3 = 1.1
y1 = f(x1)
y2 = f(x2)
y3 = f(x3)
while (np.abs(y3) > presnost): # predpokladame, ze treti bod je neblize reseni
#print('Krok ', n ,', koren ', x3 ,', hodnota ', y3)
# hodnoty y1, y2, y3 prolozime Lagrangeovym polynomem, coz lze zapsat jako L(x)=A*x^2 + B*x + C
a1 = y1/((x1-x2)*(x1-x3))
a2 = y2/((x2-x1)*(x2-x3))
a3 = y3/((x3-x1)*(x3-x2))
A = a1+a2+a3
C = x2*x3*a1 + x1*x3*a2 + x1*x2*a3
B = -(x2+x3)*a1 -(x1+x3)*a2 -(x1+x2)*a3
# hledame reseni L(x) = 0
xn = (-B+np.sqrt(B*B-4*A*C))/(2*A)
xn0 = (-B-np.sqrt(B*B-4*A*C))/(2*A)
# z korenu vybereme ten, ktery je blizsi k x3
if np.abs(xn0-x3)<np.abs(xn-x3):
xn = xn0
# iteracni predpis
x1 = x2
x2 = x3
x3 = xn
y1 = y2
y2 = y3
y3 = f(xn)
n = n+1
7.2. Soustavy nelineárních rovnic#
řešíme soustavu \(\vec{f}(\vec{x})=\vec{0}\)
přepíšeme ji do tvaru:
7.2.1. Prostá iterace#
soustavu lze přepsat do tvaru \(\vec{x}=\vec{\varphi}(\vec{x})\):
soustava má stejné řešení jako původní soustava nelineárních rovnic
iterační vzorec: \(\vec{x}^{(k+1)}=\vec{\varphi}(\vec{x}^{k})\)
#
# reseni soustavy nelinearnich rovnic metodou proste iterace
# puvodni rovnice f1, f2
def f1(x,y):# f1(x,y) = 0
return x**2 + 4*x - y**2 - 2*y -1
def f2(x,y): # f2(x,y) = 0
return x**2 + 5*y -4
# parametricke vyjadreni x,y
def phi1(x,y): # x = phi1(x,y)
return (y**2 + 2*y +1 -x**2)/4
def phi2(x,y): # y = phi2(x,y)
return (4-x**2)/5
n = 20 # pocet kroku
x0 = 0 # pocatecni odhad x
y0 = 0 # pocatecni odhad y
for i in range(n):
#zobrazeni aktualni velikosti x,y a hodnot f1, f2 v danych bodech
#print('Krok ', i ,', (x0, y0)=(', x0 ,',', y0 ,')')
#print('Krok ', i ,', f1(x0, y0)= ', f1(x0,y0))
#print('Krok ', i ,', f2(x0, y0)= ', f2(x0,y0))
#iteracni krok - vypocet z parametrickych rovnic
xn = phi1(x0,y0)
yn = phi2(x0,y0)
x0 = xn
y0 = yn
7.2.2. Newton–Raphsonova metoda#
přesné řešení \(\vec{\xi}\) vyjádříme ve tvaru \(\vec{\xi}=\vec{x}+\delta\vec{x}\)
hodnotu funkce v bodě \(\vec{\xi}\) vyjádříme pomocí Taylorovy věty: $\( f_{i}(\vec{x}+\delta\vec{x})=f_{i}(\vec{x})+\sum_{j=1}^{n}\dfrac{\partial f_{i}}{\partial x_{j}}\delta x_{j}+\mathcal{O}(\delta \vec{x}^{2}) \)$
zanedbáním \(\mathcal{O}(\delta \vec{x}^{2})\) získáme: $\( f_{i}(\vec{x}+\delta\vec{x})=f_{i}(\vec{x})+\sum_{j=1}^{n}\dfrac{\partial f_{i}}{\partial x_{j}}\delta x_{j}=0 \)$
řešíme tedy soustavu \(n\) lineárních rovnic s neznámou \(\delta \vec{x}\)
iterační vztah: \( x_{i}^{(k+1)}=x_{i}^{(k)}+ \delta x_{i}^{(k)}\)
#
# reseni soustavy nelinearnich rovnic Newton-Raphsonovou metodou
stupen = 2
# delka kroku
h = 0.01
# derivace funkce f podle x
def dfdx(f,x,y,h):
return 1/(2*h) * ( f(x+h,y) - f(x-h,y) )
# derivace funkce f podle y
def dfdy(f,x,y,h):
return 1/(2*h) * ( f(x,y+h) - f(x,y-h) )
# puvodni rovnice f1, f2
def f1(x,y):# f1(x,y) = 0
return x**2 + 4*x - y**2 - 2*y - 1
def f2(x,y):# f2(x,y) = 0
return x**2 + 5*y - 4
# pocet iteraci
n = 20
# pocatecni odhad
x0 = 1
y0 = 1
# matice A a prava strana b pro soustavu linearnich rovnic
A = np.zeros((stupen,stupen))
b = np.array((stupen,1))
for i in range(n):
#print('Krok ', i ,', (x0, y0)=(', x0 ,',', y0 ,')')
#print('Krok ', i ,', f1(x0, y0)= ', f1(x0,y0))
#print('Krok ', i ,', f2(x0, y0)= ', f2(x0,y0))
A[0,0] = dfdx(f1,x0,y0,h)
A[0,1] = dfdy(f1,x0,y0,h)
A[1,0] = dfdx(f2,x0,y0,h)
A[1,1] = dfdy(f2,x0,y0,h)
b[0] = -f1(x0,y0)
b[1] = -f2(x0,y0)
# vypocitame neznamou
dx = np.linalg.solve(A,b)
# iteracni vztah
x0 = x0 + dx[0]
y0 = y0 + dx[1]
