10. Obyčejné diferenciální rovnice (ODR)#

Naimportujeme si knihovny potřebné pro následující příklady:

import numpy as np
import matplotlib.pyplot as plt

Vektorové vyjádření systému rovnic $$ \dfrac{\mathrm{d}\vec y}{\mathrm{d}x}=\vec f (x,\vec y)$$
ODR $N$-tého řádu převádíme na soustavu $N$ diferenciálních rovnic 1. řádu
Potřebujeme $N$ počátečních podmínek
Řešení se liší v závislosti na počátečních podmínkách:
1. Počáteční problém: všechny podmínky jsou zadány v jednom bodě
2. Okrajový problém: všechny podmínky nejsou zadány v jednom bodě

10.1. Runge-Kuttovy metody pro řešení počátečního problému#

10.1.1. Eulerova metoda#

Z Taylorova rozvoje známe směrnici tečny
V každém bodě $x_{1},x_{2}\dots x_{n}$ aproximujeme funkci její tečnou $$ y(x+h)\approx y(x)+hf\left( x,y(x)\right)$$
Metodu lze zpřesnit zmenšením vzdálenosti $h=x_{k+1}-x_{k}$

10.1.2. Metoda středního bodu#

Přesnější vyjádření směrnice tečny:
1. Provedeme poloviční krok $h/2$ pomocí Eulerovy metody
2. V tomto bodě vypočítáme směrnici tečny
3. Tuto směrnici použijeme k provedení celého kroku z bodu $x$ do $x+h$ $$ y(x+h)\approx y(x)+hf\left[ x+\dfrac{h}{2},y(x)+\dfrac{h}{2}f\left( x,y(x)\right) \right] $$

10.1.3. Heunova metoda#

Opět zpřesňujeme vyjádření směrnice tečny:
1. Směrnici tečny v bodě $x+h$ určíme pomocí Eulerovy metody
2. Uděláme průměr ze směrnic v bodech $x$ a $x+h$
3. Tuto směrnici použijeme k provedení celého kroku z bodu $x$ do $x+h$ $$ y(x+h)\approx y(x)+\dfrac{h}{2}\lbrace f \left( x,y(x) \right) + f\left[x+h,y(x)+hf(x,y(x))\right]\rbrace $$

10.1.4. Runge-Kuttova metoda 4. řádu#

Využívá postupné zpřesňování hodnot derivace v bodech mezi $x$ a $x+h$
Odvození
Postup výpočtu: $$ k_{1}=f(x_{n},y_{n})$$ k_{2}=f(x_{n}+\dfrac{h}{2},y_{n}+\dfrac{h}{2}k_{1})$$ k_{3}=f(x_{n}+\dfrac{h}{2},y_{n}+\dfrac{h}{2}k_{2})$$ k_{4}=f(x_{n}+h,y_{n}+hk_{3})$$ y_{n+1}\approx y_{n}+\dfrac{h}{6}\left(k_{1}+2k_{2}+2k_{3}+k_{4} \right)$$
Pro Runge-Kuttovy metody obecně platí:
- Výhody: robustní metoda, funguje témeř vždy
- Nevýhody: na jeden krok je potřeba funkci několikrát vyčíslit, nehodí se pro řešení rovnic se silným tlumením (stiff rovnice)

Cvičení 10.01: Vyřešete modelovou úlohu popisující časový vývoj počtu bakterií $\dfrac{\mathrm{d}N}{\mathrm{d}t}=(1+\cos t)N(t)$ výše zmíněnými metodami. Předpokládáme, že na počátku žije jen jedna bakterie.

# kod

# pocatecni podminky
uH  = 1 # Heunova metoda
uSB = 1 # Metoda stredniho bodu
uE  = 1 # Eulerova metoda
uRK = 1 # Runge-Kutta

# konecny cas
T = 5

# casove kroky
tA = np.linspace(0,T,num=500)

## resime tuto rovnici f(x,y(x))=dy(x)/dx:
def f(x,y):
    return (1 + np.cos(x)) * y

# presne reseni
exact = np.exp(tA + np.sin(tA)) 

# delka kroku
h = 0.1 
##


## stiff
#def f(x,y):
#    return -15*y
#
## presne reseni
#exact = np.exp(-15*tA ) 
#
#
# delka kroku (0.1 - 0.2)
#h=0.2
##


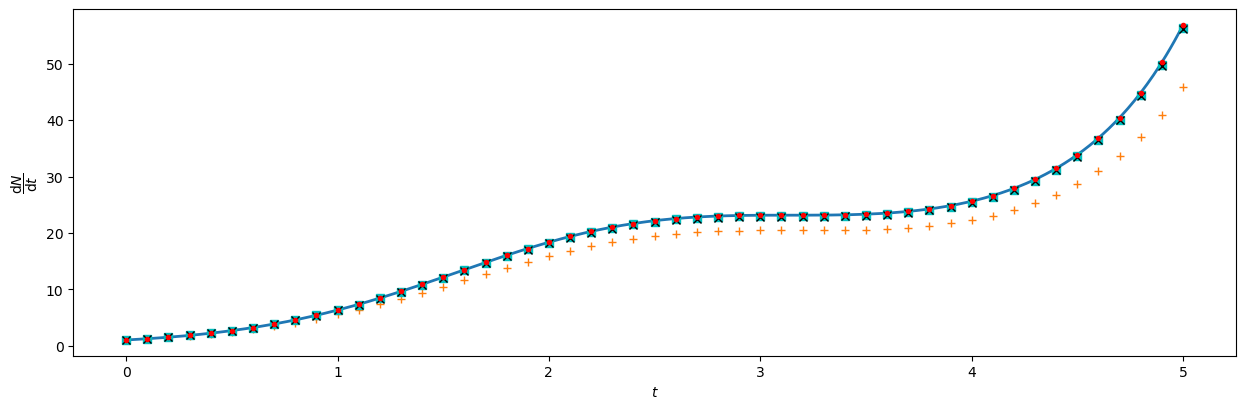
fig, ax = plt.subplots(figsize=(15,4.5))
ax.plot(tA,exact,linewidth=2) # zobrazime presne reseni

t = 0
while t<T:
    # Eulerova metoda
    ax.plot(t,uE, marker="+", color='C1')
    # spocteme novou hodnotu promenne uE
    uE = uE+h*f(t,uE)

    # Metoda stredniho bodu
    ax.plot(t,uSB, marker="s", color='c')
    # spocteme novou hodnotu promenne uSB
    uSB = uSB+h*f(t+h/2,uSB+h/2*f(t,uSB))

    # Heunova metoda
    ax.plot(t,uH, marker="x", color='k')
    # spocteme novou hodnotu promenne uH
    uH = uH+h/2*(f(t,uH)+f(t+h,uH+h*f(t,uH)))

    # Runge-Kutta 4. rad
    ax.plot(t,uRK, marker=".", color='r')
    # spocteme novou hodnotu promenne uRK
    k1 = f(t,uRK)
    k2 = f(t+h/2,uRK+h/2*k1)
    k3 = f(t+h/2,uRK+h/2*k2)
    k4 = f(t+h,uRK+h*k3)
    uRK = uRK + h/6*(k1+2*k2+2*k3+k4)
    
    t = t + h
    
ax.set_ylabel(r'$\dfrac{\mathrm{d}N}{\mathrm{d}t}$')
ax.set_xlabel(r'$t$')
#ax.set_xlim((4.5,5))
#ax.set_ylim((0,60))


# stiff rovnice
#ax.set_ylim((-1,1))

Text(0.5, 0, '$t$')

10.2. Stiff rovnice (rovnice se silným tlumením)#

Takové rovnice, které v sobě obsahují útlum s charakteristickým časem $\tau \ll $ jiný charakteristický čas úlohy
Pro řešení je potřeba zvolit délku kroku $h \leq \tau$

10.3. Řešení soustav diferenciálních rovnic#

Zadnou úlohu převedeme na soustavu $N$ diferenciálních rovnic 1. řádu

Cvičení 10.02: Runge-Kuttovou metodou čtvrtého řádu vyřešte Keplerovu úlohu dle tohoto zadání.

# kod

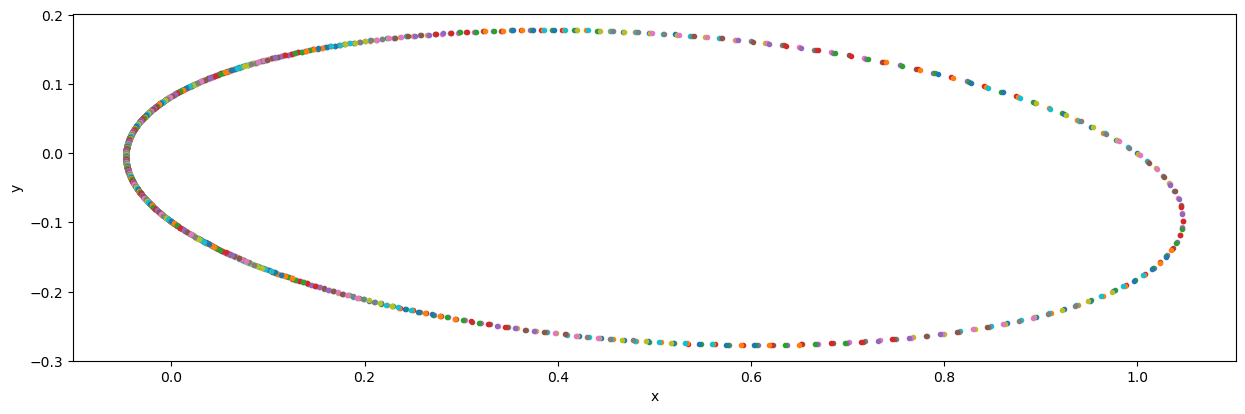
# metodou Runge-Kuta ctvrteho radu budeme resit soustavu dvou rovnic druheho radu (problem dvou teles)

# konecny cas
T = 20

# pocatecni podminky
# array([x, dx/dt, y, dy/dt])
u = np.array([1, -0.3, 0, 0.3])


def f(u):
    w = np.zeros(4)
    w[0] = u[1]
    w[1] = -u[0]/(u[0]**2+u[2]**2)**(3/2)
    w[2] = u[3]
    w[3] = -u[2]/(u[0]**2+u[2]**2)**(3/2)   
    return w

fig, ax = plt.subplots(figsize=(15,4.5))

t = 0
while t<T:    
    r = (u[0]**2+u[2]**2)**(1/2)    
    h = 1e-1*r**2
    #h = 0.005 # delka kroku
    t = t + h
    ax.scatter(u[0], u[2], marker=".")
    k1 = f(u)    
    k2 = f(u+h/2*k1)
    k3 = f(u+h/2*k2)
    k4 = f(u+h*k3)
    u=u+h/6*(k1+2*k2+2*k3+k4)
    
ax.set_xlabel('x')
ax.set_ylabel('y')

Text(0, 0.5, 'y')

Letní semestr 2023/24

Obyčejné diferenciální rovnice (ODR)

Contents