1. Jupyter notebook a základy Pythonu#

On-line interaktivní verze: Pro spuštení interaktivní verze této stránky klikněte ve vrchním menu na a zvolte Binder, ve kterém lze Jupyter notebook (JP) upravovat a následně uložit na disk.
Tip: Tento soubor je možné stáhnout kliknutím na , a to ve formě *.ipynb pro pozdější off-line editaci v prostředí Anaconda, nebo pro on-line editaci v Google Colab.

1.1. Interaktivní Jupyter notebook#

Napište print('Hello, World!') a stiskněte Shift + Enter (nebo Ctrl + Enter)

print('Hello, World')

Hello, World

Pomocí klávesy b vložíte další řádek do JP.

  • Stiskněte b.

Odstranění řádku: vyberte řádek v JP a stiskněte d + d

Klávesou a vložíte nový řádek nad právě vybraný.

  1. Stiskněte a.

  2. Vyberte tento nový řádek a stiskněte m. Nyní lze do řádku místo kódu zapisovat text,

  3. Zadávání ukončíte stisknutím kombinace Shift + Enter.

  4. Pokud chcete řádek převést na kód, stiskněte y.

Pro nápovědu stiskněte h.

1.2. Python#

Jednořádkový komentář se zadává za znak #, více řádků lze zakomentovat pomocí """ a """:

# toto je komentar
"""
Komentar
na vice
radku...
"""
print("Hello, World!") 

Hello, World!

Inicializace proměnných a, b, základní aritmetické operace a výpis výsledku pomocí funkce print():

a=43
b=5.0

soucet=a+b
rozdil=a-b
soucin=a*b
podil=a/b
mocnina=a**b
zbytek_po_deleni = a%b

# vypis
print('Soucet ',soucet)
print('Rozdil ',rozdil)
print('Soucin ',soucin)
print('Podil ',podil)
print('Mocnina ',mocnina)
print('Zbytek po deleni ',zbytek_po_deleni)

Soucet  48.0
Rozdil  38.0
Soucin  215.0
Podil  8.6
Mocnina  147008443.0
Zbytek po deleni  3.0
Cvičení 01.01: Vypočtěte objem jehlanu o stranách 3 a 4 majiícího výšku 7. 
a=3.0
b=4.0
v=7.0
S=a*b
V=1/3*S*v
print(V)

28.0

1.3. Podmínkové cykly#

1.3.1. If … else#

Pozor: vnitřní části kódu je nutné odsadit, obvykle se používají čtyři mezery.

Za klíčovými slovy if a else musíme psát :.

cislo = 0
if cislo > 0:
    print(cislo, "je kladne.")
elif cislo <0:
    print(cislo, "je zaporne")
else:
    print("musi to byt nula")    
print("Tento text se vypise vzdy.")

musi to byt nula
Tento text se vypise vzdy.

1.3.2. For …#

Zde využijeme funkci range(min,max,krok), která vytvoří sekvenci celých čísel od min po max (prvek max není v sekvenci obsažen) s uvedeným krokem. Výchozí hodnoty jsou min = 0 a krok = 1.

for x in range(10):
    print(x)

0
1
2
3
4
5
6
7
8
9

1.3.3. While…#

cislo = 0
while cislo < 10:
  print(cislo)
  cislo = cislo+1 # ekvivalenti zapis je take: cislo += 1

0
1
2
3
4
5
6
7
8
9

1.3.4. Break#

Pomocí příkazu break se ukončí probíhající cyklus. Pokud je cyklus vnořený, ukončí se pouze tento vnořený cyklus. V následujícím příkladu využijeme funkci len() která nám vrátí délku seznamu vytvořeného pomocí range().

# Ze seznamu cislic 0,1,2,... chci vypsat pouze prvni dve cislice. 
seznam_cislic = range(0,5)

for cislo in range(0, len(seznam_cislic)):
    if cislo == 2:
        break
    else:
        print('Cislo: ',seznam_cislic[cislo])
    print('Pocitadlo: ',cislo)
print("Hotovo")

Cislo:  0
Pocitadlo:  0
Cislo:  1
Pocitadlo:  1
Hotovo

1.3.5. Continue#

Příkaz continue ukončí aktuální iteraci v cyklu a pokračuje další iterací.

# Ze seznamu cislic 0,1,2,... chci vypsat vsechny cislice, krome dvojky. 
seznam_cislic = range(0,5)

for cislo in range(0, len(seznam_cislic)):
    if cislo == 2:
        continue
    else:
        print('Cislo: ',seznam_cislic[cislo])
    print('Pocitadlo: ',cislo)
print("Hotovo")

Cislo:  0
Pocitadlo:  0
Cislo:  1
Pocitadlo:  1
Cislo:  3
Pocitadlo:  3
Cislo:  4
Pocitadlo:  4
Hotovo

1.4. Funkce#

Funkce se definuje příkazem def. Následuje jméno funkce, seznam vstupních parametrů a vše je zakončené :. Tělo funkce musí být odsazené. Funkce může vrátit hodnotu pomocí příkazu return.

def objem_jehlanu(a,b,v):
  return 1/3*a*b*v

print("Objem jehlanu = ",objem_jehlanu(2,3,4))

Objem jehlanu =  8.0
Cvičení 01.02: Napište funkci, která rozhodne, zda zadané číslo je liché, nebo sudé, a vypište výsledek. 
def funkce(c):
    if cislo % 2 == 0:
        print('Cislo ',c,' je sude.')
    else:
        print('Cislo ',c,' je liche.')

cislo = 6
funkce(cislo)

Cislo  6  je sude.

1.5. Numerická knihovna numpy#

Pro import numerické knihovny numpy použijeme příkaz:

import numpy as np

1.5.1. Maticové operace#

Pole (vektor, matice) lze vytvářet pomocí funkce array():

# vektor
a = np.array([1, 2, 3])

# matice (pole)
A = np.array([[1,2,3],[4,5,6],[7,8,9]])
Pozor: v poli array má první prvek index 0!

Rozměry pole zjistíme pomocí funkce shape:

print(a.shape)
print(A.shape)

(3,)
(3, 3)

Funkce size vrátí počet prvků v poli:

print(a.size)
print(A.size)

3
9

Matici lze transponovat funkcí transpose():

A_transponovana = A.transpose()
print(A_transponovana)

[[1 4 7]
 [2 5 8]
 [3 6 9]]

Pro vytváření polí lze používat následující generátory:

  • Pomocí funkce arange() vytvoříme pole s prvky od 0 do 10 (poslední prvek není obsažen) a krokem 1:

pole = np.arange(0,10,1)
print(pole)

[0 1 2 3 4 5 6 7 8 9]

  • Pomocí funkce linspace() vygenerujeme pole s prvky od 0 do 10 (včetně), přičemž počet prvků je 20:

pole = np.linspace(0,10,20)
print(pole)

[ 0.          0.52631579  1.05263158  1.57894737  2.10526316  2.63157895
  3.15789474  3.68421053  4.21052632  4.73684211  5.26315789  5.78947368
  6.31578947  6.84210526  7.36842105  7.89473684  8.42105263  8.94736842
  9.47368421 10.        ]

  • Příkazem logspace() vytvoříme pole od 0 do 10 s počtem prvků 20 v logaritmickém měřítku (\(\log_{10}\)):

pole = np.logspace(0,10,20,base=10)
print(pole)

[1.00000000e+00 3.35981829e+00 1.12883789e+01 3.79269019e+01
 1.27427499e+02 4.28133240e+02 1.43844989e+03 4.83293024e+03
 1.62377674e+04 5.45559478e+04 1.83298071e+05 6.15848211e+05
 2.06913808e+06 6.95192796e+06 2.33572147e+07 7.84759970e+07
 2.63665090e+08 8.85866790e+08 2.97635144e+09 1.00000000e+10]

  • Pomocí funkce zeros() vytvoříme nulovou matici 2x2:

pole = np.zeros((2,2))
print(pole)

[[0. 0.]
 [0. 0.]]

  • Funkcí ones() vytvoříme jedničkovou matici 3x3:

pole = np.ones((3,3))
print(pole)

[[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]

  • Pomocí funkce eye() vytvoříme matici 3x3 s jedničkami na diagonále, ostatní hodnoty jsou nulové:

pole = np.eye(3)
print(pole)

[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

  • Pole náhodných čísel v rozmezí 0 az 1 se vygeneruje pomocí funkce np.random.rand():

pole_nahodnych_cisel = np.random.rand(3,2)
print(pole_nahodnych_cisel)

[[0.96928324 0.4717543 ]
 [0.63600405 0.75182797]
 [0.06205565 0.76172901]]

Pro přístup k prvkům pole A používáme syntaxi A[i,j], kde i je index řádku a j je index sloupce:

prvni_prvek_pole = A[0,0]
print(prvni_prvek_pole)

1

Pro přístup k prvkům pole používáme syntaxi [min:max:krok]. Mějme vektor \(\mathbf{v}=(0,1,2,3,4,5,6)\). Nyní z něj vyjmeme první (“0”) až šestý prvek (“5”), a to s krokem 2:

v = np.arange(0,7)
print(v)
vyber_z_v = v[0:6:2]
print(vyber_z_v)

[0 1 2 3 4 5 6]
[0 2 4]

Podobně u matice \(A\) vybereme např. poslední dva prvky ve třetím sloupci.

A_vyber = A[1:,2]
print(A_vyber)

[6 9]

U matice \(A\) vybereme první řádek:

prvni_radek = A[0,:]
print(prvni_radek)

[1 2 3]

U matice \(A\) vybereme první sloupec:

prvni_sloupec = A[:,0]
print(prvni_sloupec)

[1 4 7]

Násobení matic a vektorů se provádí pomocí operátoru dot:

# matice 2x3
A = np.array([[1,2,3],[4,5,6]])
print(A)
print(A.shape)

# matice 3x2
B = np.array([[1,2],[3,4],[5,6]])
print(B)
print(B.shape)

# vysledek
C = np.dot(A,B)
print(C)

[[1 2 3]
 [4 5 6]]
(2, 3)
[[1 2]
 [3 4]
 [5 6]]
(3, 2)
[[22 28]
 [49 64]]
Pozor: operace C*C násobí matice po prvcích (není to maticové násobení)
# maticove nasobeni
print(np.dot(C,C))

# nasobeni po prvcich
print(C*C)

[[1856 2408]
 [4214 5468]]
[[ 484  784]
 [2401 4096]]

1.5.2. Funkce#

numpy obsahuje často používané funkce a konstanty (napr. sqrt(), log(), log10(), sin(), abs(), e, pi, …):

print(np.sqrt(5))
print(np.log(5))
print(np.log10(5))
print(np.sin(5))
print(np.abs(-3))
print(np.e)
print(np.pi)

2.23606797749979
1.6094379124341003
0.6989700043360189
-0.9589242746631385
3
2.718281828459045
3.141592653589793

Součet prvků v poli je dán funkcí sum():

# soucet prvku v poli
soucet = np.sum(A)
print(soucet)

21

Minimální a maximální hodnotu v poli určíme funkcí min() a max():

# maximalni hodnota v poli
maximum = np.max(A)
print(maximum)

# minimalni hodnota v poli
minimum = np.min(A)
print(minimum)

6
1

Funkce average() vrací průměrnou hodnotu; std() je směrodatná odchylka a var() je rozptyl:

# prumerna hodnota
prumer = np.average(A)
print(prumer)

# smerodatna odchylka
smerodatna_odchylka = np.std(A)
print(smerodatna_odchylka)

# rozptyl
rozptyl = np.var(A)
print(rozptyl)

3.5
1.707825127659933
2.9166666666666665

Index prvku v poli lze najít pomocí funkce argwhere():

index_hledaneho_prvku = np.argwhere(A == 3)
print(index_hledaneho_prvku)

[[0 2]]
Tip: Další příklady a návody pro práci s knihovnou numpy lze nalézt na https://numpy.org/.

1.6. Visualizace dat#

Pro kreslení grafů využijeme knihovnu matplotlib.pyplot:

import matplotlib.pyplot as plt

1.6.1. Graf jedné proměnné#

Vygenerujeme \(x\) a \(y\) hodnoty pro funkci sin():

x = np.linspace(0,4*np.pi,100)
y = np.sin(x)

Nejdříve je potřeba vytvořit obrázek pomocí fig. Vykreslení dat provedeme příkazem plot():

fig, ax = plt.subplots()
ax.plot(x,y)

[<matplotlib.lines.Line2D at 0x778d4337ff40>]
_images/Cviceni01vyplnene_99_1.png

Přidáme popisky os pomocí set_xlabel(), set_ylabel() a název grafu pomocí set_title():

fig, ax = plt.subplots()
ax.plot(x,y)
ax.set_xlabel('x')
ax.set_ylabel('sin(x)')
ax.set_title('Graf funkce sin(x)')

Text(0.5, 1.0, 'Graf funkce sin(x)')
_images/Cviceni01vyplnene_101_1.png

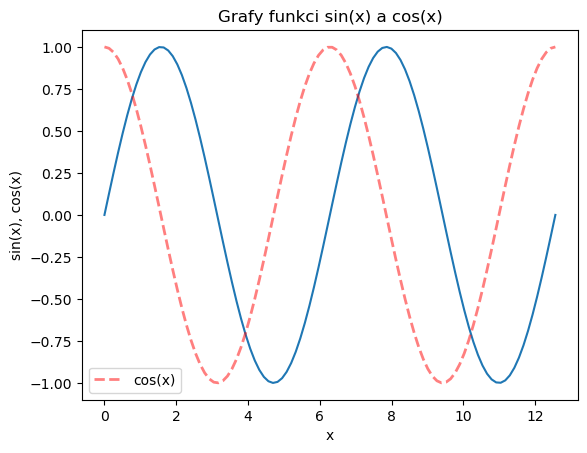
Přidáme funkci cos(), nastavíme barvu (color), styl (linestyle) a šířku (linewidth) linky. Průhlednost se nastavuje parametrem alpha. Legendu zobrazíme příkazem legend():

# funkce cos()
y1 = np.cos(x)

fig, ax = plt.subplots()
ax.plot(x,y)

# vykreslime funkci cos()
ax.plot(x,y1, color='red',linestyle='dashed',linewidth=2,label='cos(x)',alpha=0.5)


ax.set_xlabel('x')
ax.set_ylabel('sin(x), cos(x)')
ax.set_title('Grafy funkci sin(x) a cos(x)')
ax.legend()

<matplotlib.legend.Legend at 0x778d432157c0>
_images/Cviceni01vyplnene_103_1.png

Na závěr obrázek uložíme příkazem savefig():

fig.savefig("obrazek.png", dpi=300)

1.6.2. Visualizace závislosti dvou proměnných#

Mějme funkci \(z(x,y)\), která závisí na dvou proměnných \(z(x,y)=\exp(-\sqrt{x^2+y^2})\cos(2x)\sin(2y)\), a vykreslíme její závislost v 2D grafu.

Vytvoříme mřížku \(x\times y\) pomocí funkce meshgrid():

fig, ax = plt.subplots()
osa_x = np.linspace(-2, 2, 50)
osa_y = np.linspace(-2, 2, 50)
(x,y) = np.meshgrid(osa_x,osa_y)
_images/Cviceni01vyplnene_109_0.png

Spočítáme hodnoty funkce \(z(x,y)\):

z = np.exp(-np.sqrt(x**2+y**2))*np.cos(2*x)*np.sin(2*y)

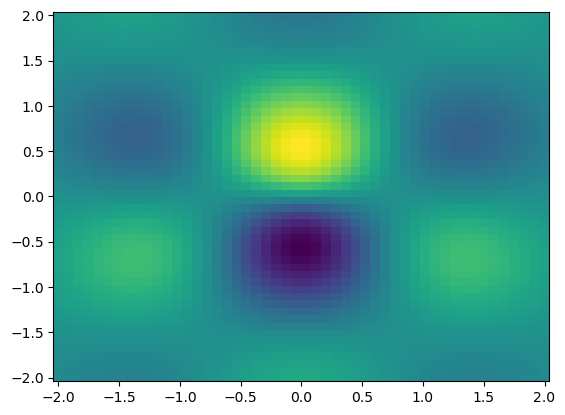
2D graf vykreslíme pomocí funkce pcolor() s parametrem shading='auto':

fig, ax = plt.subplots()
osa_x = np.linspace(-2, 2, 50)
osa_y = np.linspace(-2, 2, 50)
(x,y) = np.meshgrid(osa_x,osa_y)
z = np.exp(-np.sqrt(x**2+y**2))*np.cos(2*x)*np.sin(2*y)
ax.pcolor(x,y,z,shading='auto')

<matplotlib.collections.PolyCollection at 0x778d4271e880>
_images/Cviceni01vyplnene_113_1.png

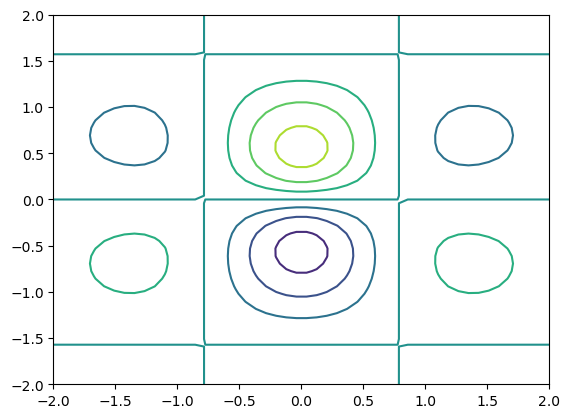
Kontury získáme použitím funkce contour():

fig, ax = plt.subplots()
osa_x = np.linspace(-2, 2, 50)
osa_y = np.linspace(-2, 2, 50)
(x,y) = np.meshgrid(osa_x,osa_y)
z = np.exp(-np.sqrt(x**2+y**2))*np.cos(2*x)*np.sin(2*y)
ax.contour(x,y,z)

<matplotlib.contour.QuadContourSet at 0x778d425445b0>
_images/Cviceni01vyplnene_115_1.png

1.6.3. 3D visualizace#

Máme stejnou funkci \(z(x,y)=\exp(-\sqrt{x^2+y^2})\cos(2x)\sin(2y)\), kterou nyní chceme vykreslit v 3D grafu. Nejdříve vytvoříme trojrozměrnou osu:

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
_images/Cviceni01vyplnene_118_0.png

Vytvoříme mřížku \(x\times y\) pomocí funkce meshgrid:

osa_x = np.linspace(-2, 2, 50)
osa_y = np.linspace(-2, 2, 50)
(x,y) = np.meshgrid(osa_x,osa_y)

Spočítáme hodnoty funkce \(z(x,y)\):

z = np.exp(-np.sqrt(x**2+y**2))*np.cos(2*x)*np.sin(2*y)

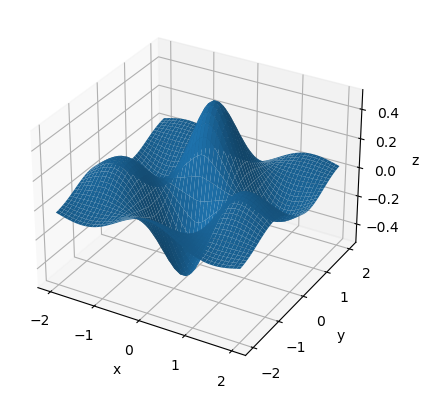
3D data vykreslíme pomocí funkce plot_surface() a přidáme popisky os:

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')

osa_x = np.linspace(-2, 2, 50)
osa_y = np.linspace(-2, 2, 50)
(x,y) = np.meshgrid(osa_x,osa_y)
z = np.exp(-np.sqrt(x**2+y**2))*np.cos(2*x)*np.sin(2*y)

ax.plot_surface(x, y, z)
ax.set(xlabel='x', ylabel='y', zlabel='z')

[Text(0.5, 0, 'x'), Text(0.5, 0.5, 'y'), Text(0.5, 0, 'z')]
_images/Cviceni01vyplnene_124_1.png
Cvičení 01.03: Vykreslete průběh funkce log(x) pro x od 0.1 do 10. Osy grafu popište, přidejte legendu a obrázek uložte ve formátu *.jpg.
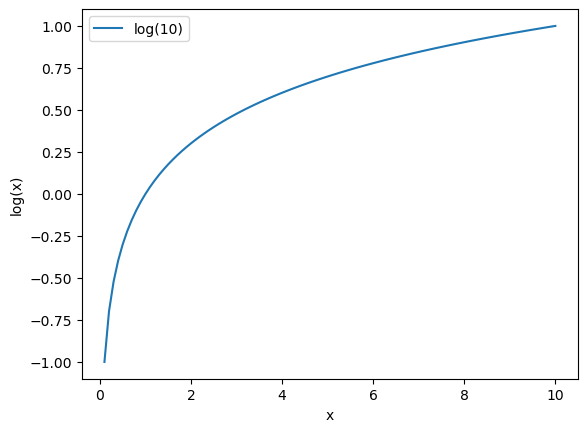
x = np.linspace(1e-1,10,100)
y = np.log10(x)
fig, ax = plt.subplots()
ax.plot(x,y,label='log(10)')
ax.set_xlabel('x')
ax.set_ylabel('log(x)')
ax.legend()
fig.savefig('log10.jpg',dpi=100)
_images/Cviceni01vyplnene_126_0.png
Tip: Další příklady a návody pro práci s knihovnou matplotlib lze nalézt na https://matplotlib.org/.