11. Obyčejné diferenciální rovnice (ODR) II

Naimportujeme si knihovny potřebné pro následující příklady:

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

• ODR \(N\)-tého řádu převádíme na soustavu \(N\) diferenciálních rovnic 1. řádu

• Potřebujeme \(N\) počátečních podmínek

• Řešení se liší v závislosti na počátečních podmínkách:

  1. Počáteční problém: všechny podmínky jsou zadány v jednom bodě (Cvičení 10)

  2. Okrajový problém: všechny podmínky nejsou zadány v jednom bodě (Cvičení 11)

• Příklad:

• Máme rovnici 2. řádu \( y''(t)=-y(t) \)

• Potřebujeme dvě počáteční podmínky:

  1. Počáteční problém (Cvičení 10)

  • všechny podmínky jsou zadány v jednom bodě \(t_{0}\)

  • \( y(t_{0})=y_{0} \) a \( y'(t_{0})=v_{0} \)

  1. Okrajový problém (Cvičení 11)

  • všechny podmínky nejsou zadány v jednom bodě

  • \( y(t_{0})=y_{0} \) a \( y(t_{1})=y_{1} \)

11.1. Metody řešení okrajových úloh:

1. Metoda střelby

2. Metoda sítí (konečných diferencí)

3. Variační metody

11.1.1. Metoda střelby

• Úlohu převedeme na ekvivalentní úlohu počátečního problému (zvolíme si parametrickou počáteční podmínku v okrajovém bodě)

• Počáteční problém umíme vyřešit postupem uvedeným na Cvičení 10

• Zkontrolujeme, zda získané řešení splňuje okrajovou podmínku s dostatečnou přesností

• Pokud ne, postup opakujeme pro jinou hodnotu paramteru

• Pro zpřesňování parametru můžeme použít např. metodu půlení intervalu

Cvičení 11.01: Jaká má být počáteční rychlost $v_{0}$ meteorologické raketové sondy (ve vakuu), aby po 5 s byla ve výšce 50 m? [1]

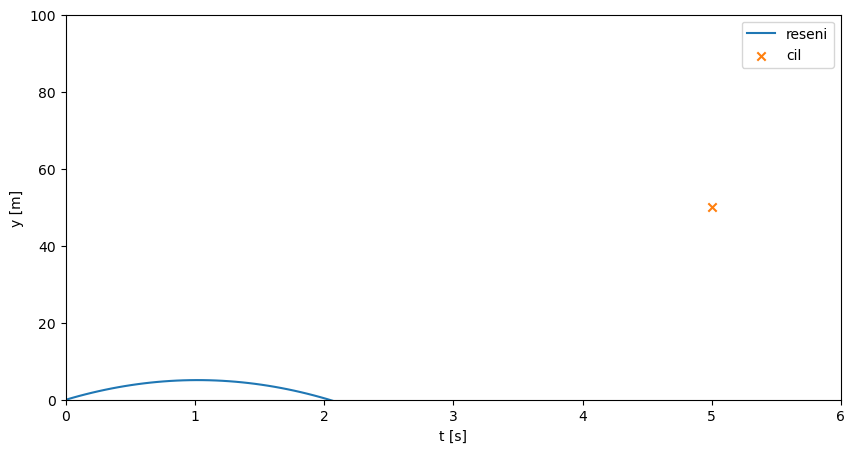
• Řešíme úlohu \(y''(t)=-g\), kde \(g\) je gravitační konstanta (speciální případ šikmého vrhu)

• Okrajové podmínky jsou \(y(t=0)=0\) a \(y(t=5)=50\), tj. podmínky jsou zadány v dvou různých okrajových bodech \(t=0\) a \(t=5\)

• Postup:

  1. Zvolíme \(v_{0}\), čímž úlohu převedeme na počáteční problém, neboť \(v_{0}=y'(t=0)\)

  2. Vypočítáme \(y(t=5)\)

  3. Pokud jsme netrefili zadanou okrajovou podmínku \(y(t=5)=50\), opakujeme výpočet pro jinou hodnotu \(y'(t=0)\)

# vstupni matice pro reseni pocatecniho problemu - resime dve rovnice prvniho radu
def F(t,s):
    return np.dot(np.array([[0,1],[0,-9.81/s[1]]]),s)    

# prvni pocatecni podminka y(t=0)=0
y0 = 0

# odhad pocatecni rychlosti rakety
v0 = 10

# cas
t_rozsah = np.linspace(0, 5, 100)
# reseni pocatecniho problemu pomoci integrovane funkce solve_ivp() pro pocatecni podminky y0 a v0
# funkce vrati hodnoty promenne t a prislusna reseni: y = y[0], y'= y[1]
reseni = solve_ivp(F, [0, 5], [y0, v0], method='RK45', t_eval = t_rozsah)

fig, ax = plt.subplots(figsize=(10,5))
ax.plot(reseni.t, reseni.y[0],label='reseni')
ax.scatter(5, 50, marker='x',color='C1',label='cil')
ax.set_xlabel('t [s]')
ax.set_ylabel('y [m]')
ax.set_xlim(0,6)
ax.set_ylim(0,100)
ax.legend()

<matplotlib.legend.Legend at 0x7d40ae123c10>

11.1.2. Metoda sítí (konečných diferencí)

• Příklad